はじめに
Go言語はサーバーサイド開発でよく使われる言語ですが、Pub/Subを用いたシステムを扱う際にも便利なライブラリや機能が提供されています。特に、Google Cloud Pub/SubのHigh-Level Client ライブラリは、Go開発者にとって使いやすく、強力な機能を提供してくれます。
前回は言語によらず Cloud Pub/Sub で意識することをまとめました。
この記事では技術的な側面に焦点を当て、Go言語でのPub/Sub Client ライブラリの効果的な使用方法について掘り下げていきたいと思います。
Low-Level APIとHigh-Levelクライアントライブラリの違い
Pub/Subシステムには、基本的に二つのAPIレベルが存在しています。Low-Level APIは、メッセージングシステムの細かいコントロールを可能にしますが、その分複雑さが増します。一方で、High-Level Client ライブラリは、開発者がより簡単にシステムを構築できるように設計されています。公式ドキュメントにもあるように、基本的にHigh-Levelクライアントを利用することが推奨されています。
Most subscriber clients don't make these requests directly. Instead, the clients rely on the Google Cloud-provided high-level client library that performs streaming pull requests internally and delivers messages asynchronously. For a subscriber client that needs greater control over how messages are pulled, Pub/Sub uses a low-level and automatically generated gRPC library.
ref: Pull subscriptions | Cloud Pub/Sub Documentation | Google Cloud
一方で、この抽象化さらたAPIを利用する際は、システムの内部動作についての理解不足が予期せぬ挙動やパフォーマンスの問題を引き起こす可能性があります。そのため、本記事では、High-Level Client ライブラリを効果的に使用するための知識とノウハウを、具体的な事例を交えながらまとめていきたいと思います。
Receive メソッドについて
goroutine の活用
Google Cloud Pub/Sub Client ライブラリで提供されているReceiveメソッドは呼び出し元をblockし、デフォルトでは内部で複数の goroutine を立ち上げ、Pub/Subからメッセージを非同期に受信します。
Receive calls f concurrently from multiple goroutines. It is encouraged to process messages synchronously in f, even if that processing is relatively time-consuming; Receive will spawn new goroutines for incoming messages, limited by MaxOutstandingMessages and MaxOutstandingBytes in ReceiveSettings.
ref: Cloud PubSub - Package cloud.google.com/go/pubsub (v1.32.0) | Go client library | Google Cloud
設定を変更することで、内部でgoroutineを一つだけ立ち上げ、同期的にメッセージを受信することも可能です。Receive内部コードだとこの辺でgoroutineの数を制御しています。
var numGoroutines int switch { case s.ReceiveSettings.Synchronous: numGoroutines = 1 case s.ReceiveSettings.NumGoroutines >= 1: numGoroutines = s.ReceiveSettings.NumGoroutines default: numGoroutines = DefaultReceiveSettings.NumGoroutines }
ack_deadline の自動変更機能
まず、Pub/Sub には Acknowledge deadline を Subscription 単位で設定できます。この deadline をすぎても Acknowledge されないメッセージは再送されます。
ref: Subscription properties | Cloud Pub/Sub Documentation | Google Cloud
ただし、この deadline は client ライブラリから変更できることに注意が必要です。
The Pub/Sub high-level client libraries provide lease management as a feature that automatically extends the deadline of a message that has not yet been acknowledged
ref: Extend ack time with lease management | Cloud Pub/Sub Documentation | Google Cloud
Go の Client ライブラリはメッセージを受信した直後に、sendModAck() を通して ModifyAckDeadline リクエストを送ります。コードだとこの辺です。つまり、受信したすべてのメッセージに対して ModifyAckDeadline リクエストしています。実際に延長する時間はこれまで Acknowledge するまでにかかった時間の99%タイルを採用しています。
Message.Nack() の内部挙動
Message には Ack と Nack という2種類の関数があり、Receive関数内でこのどちらかを必ず呼ぶ必要があります。
If received in the callback passed to Subscription.Receive, client code must call Message.Ack or Message.Nack when finished processing the Message.
ref: Cloud PubSub - Package cloud.google.com/go/pubsub (v1.32.0) | Go client library | Google Cloud
Message.Ack はメッセージを acknowledge しているのだと想像がつきますし、実際に low-level API に Acknowledge というメソッドがあるので、これをラップしていると考えることができます。
一方で、Nackに相当する rpc は存在しません。実は client 側でこのメソッドを呼び出すと、ModifyAckDeadlineRequest を ack_deadline_seconds=0 で送信しています。コードだとこの辺です。
if sendNacks { // Nack indicated by modifying the deadline to zero. it.sendModAck(nacks, 0, false) }
つまり、前の節で紹介した ack_deadline の自動変更を利用し、即時に再送するようにリクエストをしていることになります。
MaxOutstandingMessages による flow control
Go言語の Client ライブラリでは MaxOutstandingMessages という設定項目があります。これは Receive メソッドが同時に処理できるメッセージ数の上限を設定します。
MaxOutstandingMessages is the maximum number of unprocessed messages
ref: Cloud PubSub - Package cloud.google.com/go/pubsub (v1.32.0) | Go client library | Google Cloud
デフォルト設定は1000に設定されているのですが、外部リソースへのアクセスやアプリケーションリソースの様子を見て適宜設定を変更することをお勧めします。
[要確認] バッチによる retry
Pub/Sub メッセージはバッチで送信されるため、バッチに含まれるメッセージが再送される時、そのメッセージのみではなくバッチに含まれるすべてのメッセージが再送される。との記載がありましたが、公式ドキュメントやQAフォームからはその内容を確認することができませんでした。
Messages in Pub/Sub are delivered in batches, so not only the expired messages will be redelivered but also the ones belonging to these messages batches.
ローカルで256件のメッセージを receive するテストを走らせて、 goroutine の数を runtime/trace パッケージで解析したところ、Acknowledge している goroutine は受信したメッセージ数よりも少ないです。(traceパッケージについてはこちらの記事を参考にました。)
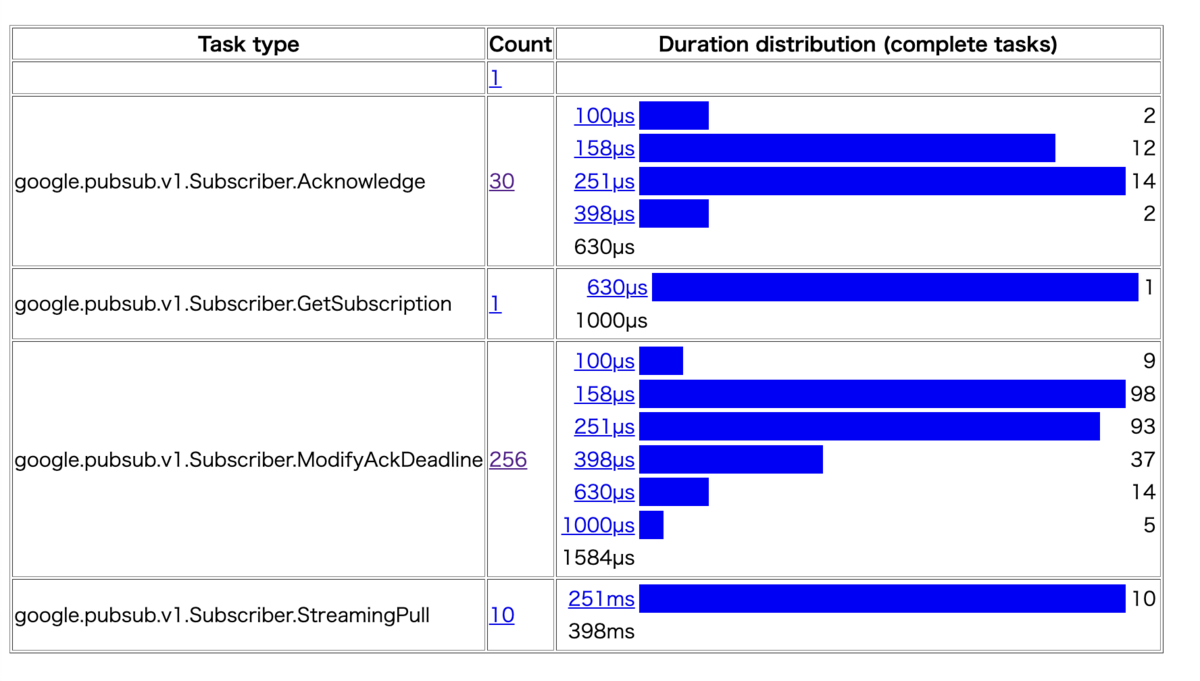
コードを確認すると、確かにAcknowledgeする部分はバッチで呼ばれていることが分かります。なのでリトライメカニズムもバッチ処理していている可能性はありそうですが、確証は得られませんでした。もし何かご存知の人がいたら教えてください。
for len(ackIDs) > 0 { toSend, ackIDs = splitRequestIDs(ackIDs, ackIDBatchSize) recordStat(it.ctx, AckCount, int64(len(toSend))) addAcks(toSend) // Use context.Background() as the call's context, not it.ctx. We don't // want to cancel this RPC when the iterator is stopped. cctx2, cancel2 := context.WithTimeout(context.Background(), 60*time.Second) defer cancel2() err := it.subc.Acknowledge(cctx2, &pb.AcknowledgeRequest{ Subscription: it.subName, AckIds: toSend, })


![【Amazon.co.jp限定】 ロジクール ワイヤレス トラックボール MX ERGO MXTB1d Bluetooth Unifying 無線 8ボタン 高速充電式 windows mac iPad OS Chrome マウス 国内正規品 [ Amazon.co.jp限定 壁紙ダウンロード付き ] 【Amazon.co.jp限定】 ロジクール ワイヤレス トラックボール MX ERGO MXTB1d Bluetooth Unifying 無線 8ボタン 高速充電式 windows mac iPad OS Chrome マウス 国内正規品 [ Amazon.co.jp限定 壁紙ダウンロード付き ]](https://m.media-amazon.com/images/I/313Dj-W0S7L._SL500_.jpg)






