Must Be Rectangular!
問題はこちら
考え方
解説放送が一番わかりやすいと思うので、そちらを見ると良い。
https://www.youtube.com/watch?v=XI8exXVxZ-Qwww.youtube.com
座標を二部グラフで捉えるという考え方は典型らしい。
下記の座標を、x座標とy座標をそれぞれ頂点としてもつ二部グラフで考えてみると、長さ3のpathが存在する場合は、その始点と終点を結ぶことで新たな頂点が追加されることになる。
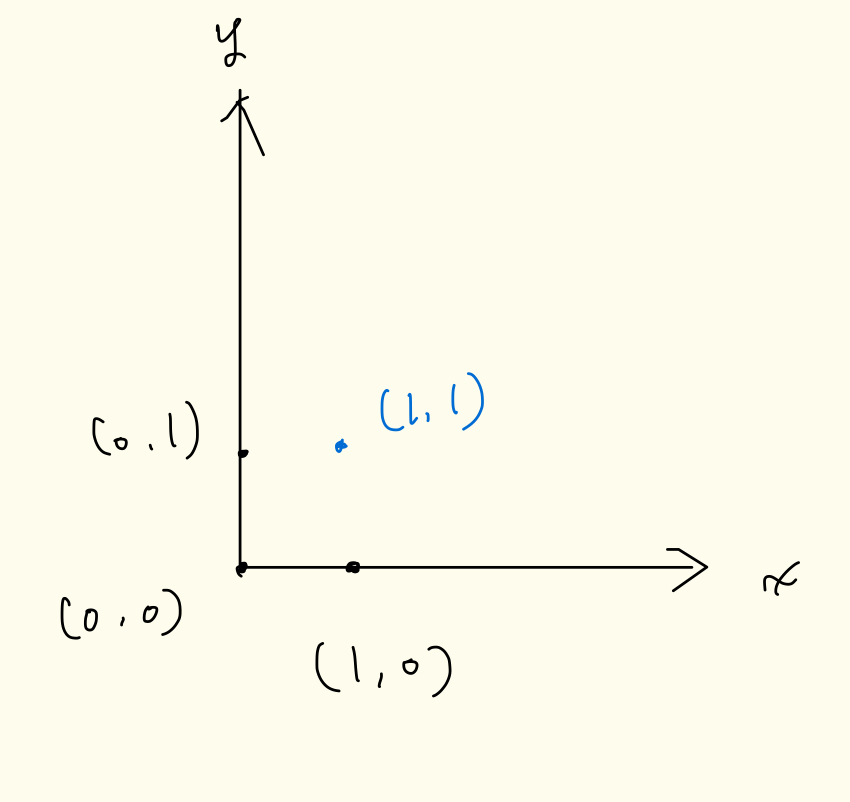
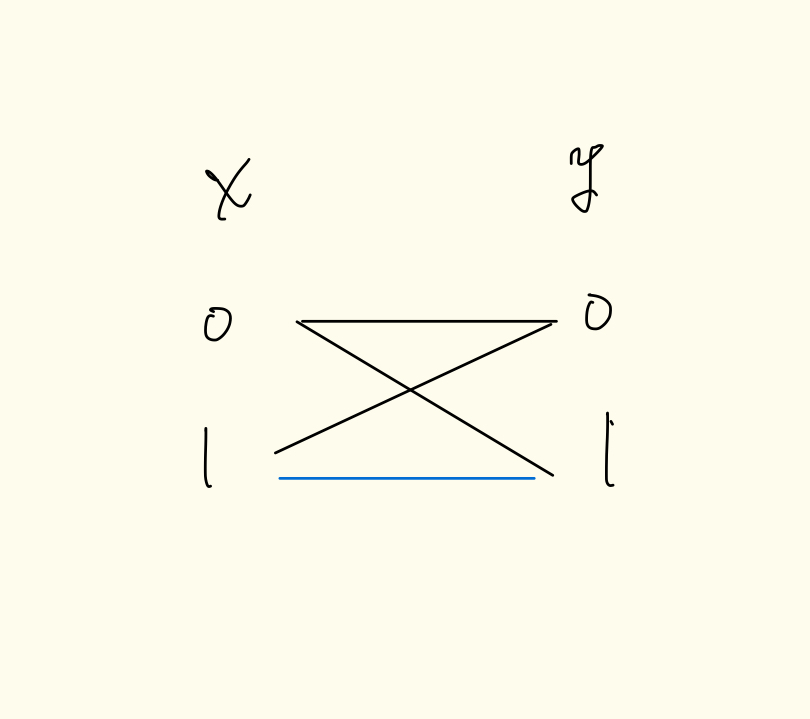
また、連結成分に関しては、その部分が完全二部グラフになるまで辺を追加することができる。これは長さが3より大きいところに関しては長さ3になるようにpathを調整することで新たに辺を追加することが可能になるから。
完全二部グラフを作るための辺の数は、それぞれのグループに属する頂点数を掛け算すれば良い。答えは新たに張ることのできる辺の数なので、答えは以下のようになる。
連結成分のx座標の個数 * 連結成分のy座標の個数 - もともと存在していた辺の数n
解答
解説放送を聞いて実装上のテクニック
- 二部グラフの表現の方法。
x座標: x、y座標: y + MAXVとすることでいつものグラフ構造を用いながら、二部グラフを表現することができる。 - 連結成分の数の保持の方法。大きさ2のvectorを用意し、
cnt[e / MAXV]++とすることで、今見ている頂点がx座標に属するかかy座標に属するかを場合分けしている。
抜粋部分
#include <bits/stdc++.h> using namespace std; typedef long long ll; #define rep(i, n) for(ll i = 0; i < (ll)(n); i++) #define each(i, mp) for(auto& i:mp) const ll MAXV = 1e5 + 5; vector<ll> xy[MAXV * 2]; vector<ll> cnt; bool visited[MAXV * 2]; void dfs(ll now) { visited[now] = true; each(e, xy[now]) { if (visited[e]) continue; cnt[e / MAXV]++; dfs(e); } } int main() { ll n; cin >> n; rep(i, n) { ll x, y; cin >> x >> y; xy[x].emplace_back(y + MAXV); xy[y + MAXV].emplace_back(x); } ll ans = 0; rep(i, MAXV * 2) { if (visited[i]) continue; cnt = vector<ll>(2); cnt[i / MAXV]++; dfs(i); ans += cnt[0] * cnt[1]; } cout << ans - n << endl; return 0; }