【因果推論】介入と調整化公式

介入とは
調整とは

介入と調整化公式

こちらの第3章前半です。

入門統計的因果推論

作者:Judea Pearl,Madelyn Glymour,Nicholas P. Jewell
朝倉書店

Amazon

介入とは

介入によってある変数の値を固定するということは、その変数が自然に変化する余地をなくすということである。つまりグラフィカルモデル上は、固定した変数に入ってくるエッジを全て取り除く操作を行う。

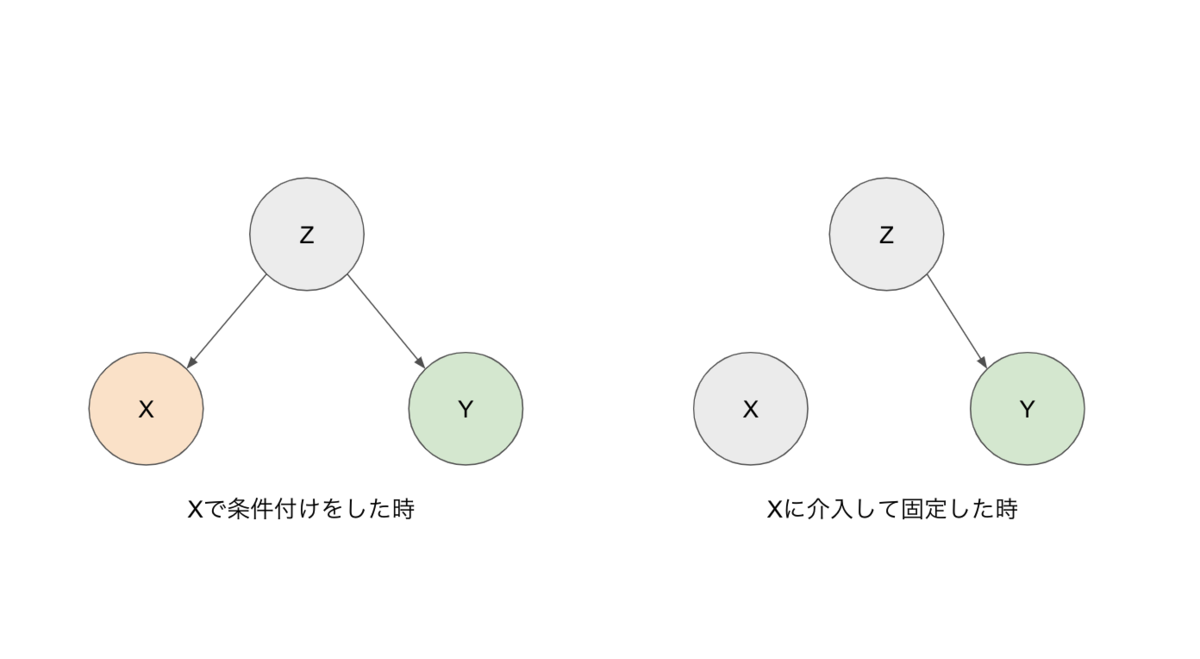
f:id:thescript1210:20211225185827p:plain:w500

条件付けした（観測した）場合と、介入した場合とではグラフィカルモデルの依存関係が全く異なることに注意が必要。

変数 $X=x$ に固定する場合を $do(X=x)$ と表記する。つまり、以下のような違いが生じる。

$P(Y=y|X=x)$ は $X＝x$ で条件付けした場合に $Y=y$ となる確率を表す。
$P(Y=y|do(X=x))$ は介入により、 $X=x$ で固定された場合に $Y=y$ となる確率を表す。

調整とは

調整化公式

以下のような図を考える。

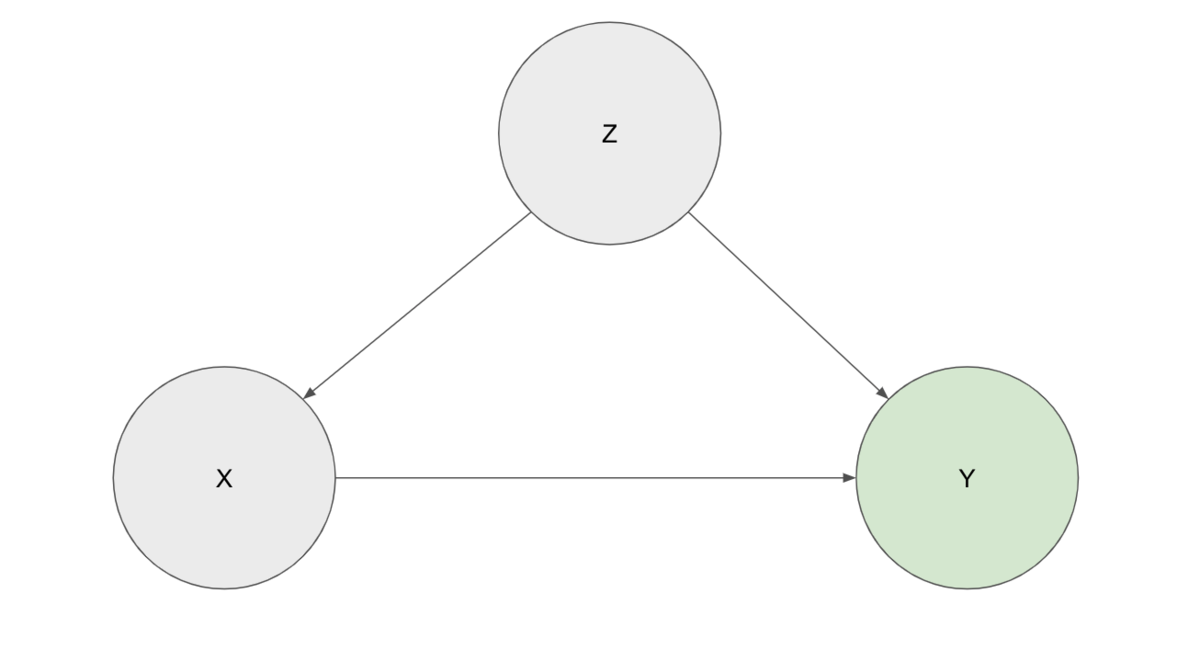
f:id:thescript1210:20211225185945p:plain:w500

変数はそれぞれ以下を表している。

$X$ : 薬の投与
$Y$ : 回復
$Z$ : 性別

新薬がどれほど効果的かを調べたい。この時は、以下のようなステップで推定を行う

患者全員に新薬を投与する介入を仮定する。これを $do(X=1)$ とする。
患者全員に薬を投与しない介入を仮定する。これを $do(X=0)$ とする。
ここでの目的は、平均因果効果（ACE: average causal effect）を推定することである。
${ P(Y=1|do(X=1)) - P(Y=1|do(X=0)) }$

因果効果 $P(Y=y|do(X=x))$ は、次図のようにグラフィカルモデルを修正した場合における条件付き確率、 $P_{m}(Y=y|X=x)$ に等しい。

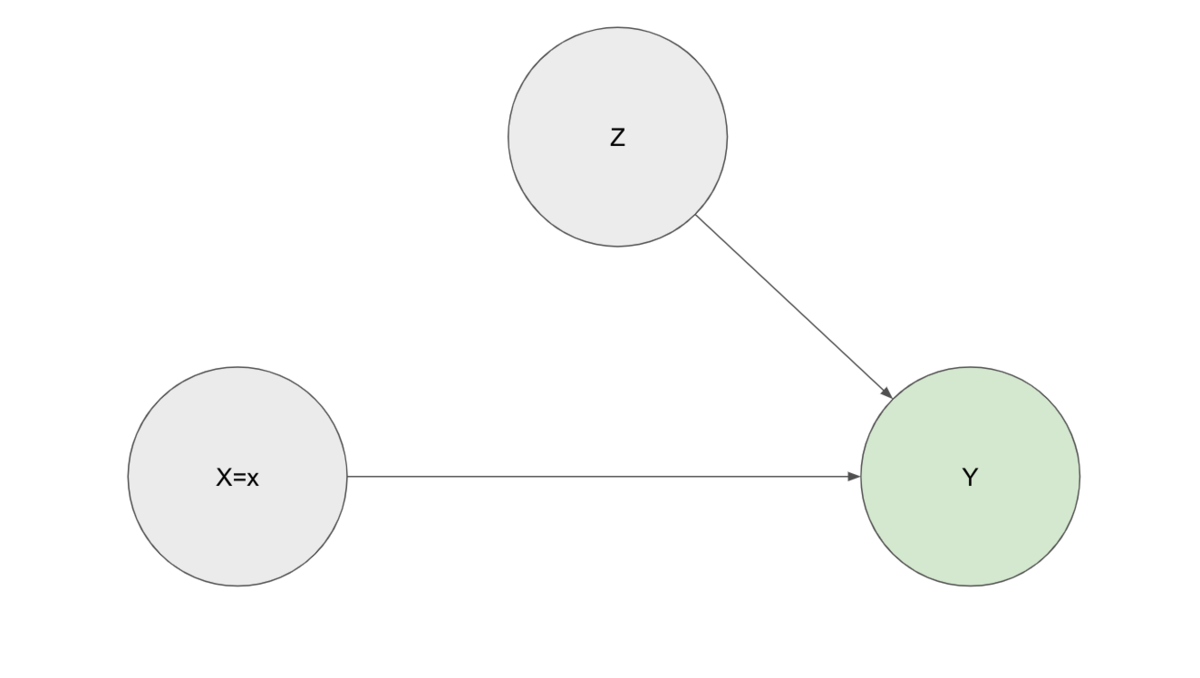
f:id:thescript1210:20211225190019p:plain:w500

まずは、介入前後で影響を受けていない確率があり、以下の二つの等式が成り立つことに注意する。

${ P_{m}(Y=y|Z=z, X=x) = P(Y=y|Z=z, X=x) \\ P_{m}(Z=z) = P(Z=z) }$

また、修正後のモデルにおいて $Z$ と $X$ はd分離されているので、独立である。これらのことより、

${ \begin{eqnarray} P(Y=y|do(X=x)) &=& P_{m}(Y=y|X=x) \\ &=& \sum_{z}P_{m}(Y=y|X = x, Z = z)P_{m}(Z=z | X = x) \\ &=& \sum_{z}P_{m}(Y=y|X=z, Z=z)P_{m}(Z=z) \end{eqnarray} }$

最後に介入前後で確率が変わらないことに注意すれば、因果効果を修正前のモデルに表れている確率を使って表現することができる。

${ P(Y=y|do(X=x)) = \sum_{z}P(Y=y | X=x, Z=z)P(Z=z) }$

この式は 調整化公式 と呼ばれる。

Simpsonの例

	薬投与	薬投与なし
男性	81/87が回復 (93%)	234/270が回復 (87%)
女性	192/263が回復 (73%)	55/80が回復 (69%)
合計	273/350が回復 (78%)	289/350が回復 (83%)

男女別で見ると薬を投与した方が回復率が高いが、男女合わせて回復率を見ると、なんと薬を投与した方が回復率が下がるという結果になっている。これは実は前の画像のように、薬に関係なく女性の方が男性よりも回復しにくいという、「性別」という変数が影響を及ぼしている事による。

調整化公式を早速当てはめて考えてみる。ここで、 $X=1$ は薬が投与されたこと、 $Z=1$ は患者が男性であること、 $Y=1$ は患者が回復したことを表す。

${ \begin{eqnarray} P(Y=1 | do(X=1)) &=& P(Y=1|X=1,Z=1)P(Z=1) + P(Y=1|X=1,Z=0)P(Z=0) \\ &=& 0.93\frac{87 + 270}{700} + 0.73\frac{263+80}{700} \\ &=& 0.832 \\ P(Y=1| do(X=0)) &=& 0.87\frac{87+270}{700} + 0.69\frac{263+80}{700} \\ &=& 0.7818 \end{eqnarray} }$