ひらめの日常

日常のメモをつらつらと

トップ > 因果推論 > 【因果推論】媒介された影響の排除

【因果推論】媒介された影響の排除

因果推論 統計 グラフィカルモデル

こちらの第3章後半です

入門 統計的因果推論

入門 統計的因果推論

Amazon

媒介

ある変数が別の変数に影響を与える場合、直接影響を与える場合と間接的に影響を与える場合とが存在し、この二つを分離することは一般的には難しい。間接的な影響のことを、媒介された影響と呼ぶ。

例として、採用に性別による差別が存在するかどうか調査したいとする。今回は以下の4つの変数が関わっているとし、XからYへの直接的な効果を計測したい。

  • X: 性別
  • Y: 採用
  • Z: 資格
  • I: 収入
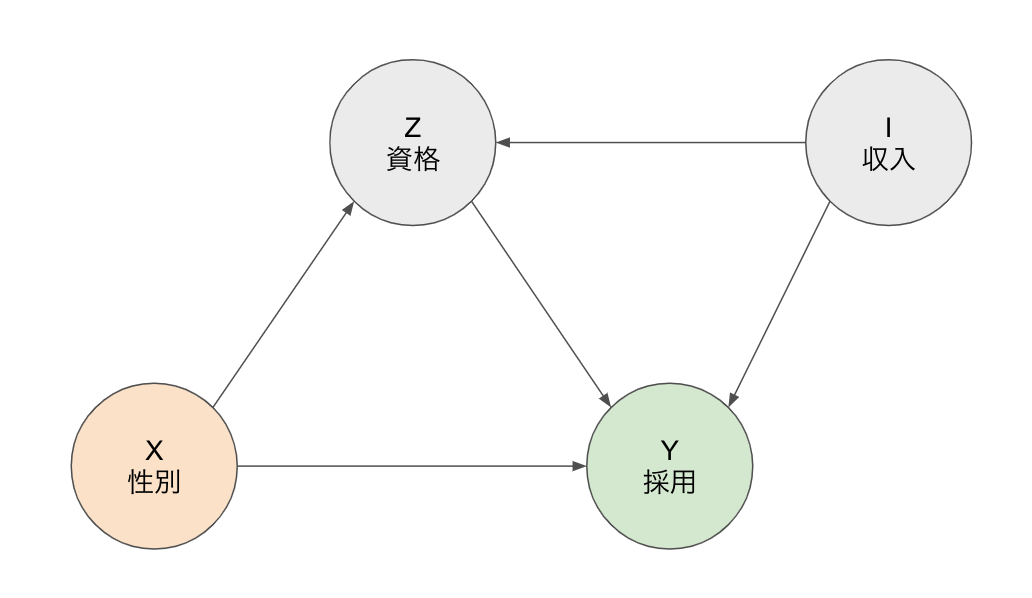
f:id:thescript1210:20220410235828p:plain:w500

まず資格について条件付けをする場合を考えてみる。条件付けするというのはつまり、P(採用決定|男性, 資格あり) とP(採用決定|女性, 資格あり)を比べるということだ。この二つに差があれば、性別が採用決定に影響を及ぼしていると判断することができる。

しかし、今回のように収入I という交絡因子を含む場合は条件付けによって比べることはできない。なぜなら、資格Z で条件づけることによって、Z と Y が I と通じて従属になってしまうためだ。（資格Z を条件付けするために収入I に影響を及ぼし、収入I が採用Y へと影響を及ぼすため。）

であれば、資格Z について条件付けをする代わりに、資格を固定すれば良い。変数を固定するのは、他の変数がどんな値を取ろうとも、その値に固定されるという意味であり、その変数に向かう矢印を全て削除することと同義である。

介入と固定に関しては過去記事を参照

hiramekun.hatenablog.com

したがって、今回の場合の直接効果、CDE (controlled direct effect) は以下で定義される。

{ CDE = P(Y=採用決定|do(X=男性), do(Z=資格あり)) - P(Y=採用決定|do(X=女性), do(Z=資格あり)) }

より一般的に、Z が X と Y の間の媒介変数である時、X の値を x から x\prime に変化させたときの Y のCDEは

{ CDE = P(Y=y|do(X=x), do(Z=z)) - P(Y=y|do(X=x\prime), do(Z=z)) }

となる。

これは、I について調整することで次のように式変形ができる。

{ \begin{eqnarray} CDE &=& P(Y=y|X=x, do(Z=z)) - P(Y=y|X=x\prime, do(Z=z)) \\ &=& \sum_{i}\left[P(Y=y|X=x, Z=z, I=i) - P(Y=y|X=x\prime, Z=z, I=i)\right]P(I=i) \end{eqnarray} }