ひらめの日常

日常のメモをつらつらと

トップ > R > RでKLダイバージェンスを描画する

RでKLダイバージェンスを描画する

R 統計

今回はRでKLダイバージェンスを描画します。
KLダイバージェンスとは、カルバック・ライブラー情報量の略称。2つの確率分布の差異を測る距離的尺度として捉えることができます。

と言われても実感がわかないと思うので、実際に描画して感覚を掴んでいきたいと思います。
実装はこちらにあります。
7/5:リンク先更新しました。

github.com

定義

まずはエントロピーの説明をし、その上にあるKLダイバージェンスの定義を述べます。

エントロピー

連続関数のエントロピーは、情報量の期待値という定義なので次のように表せます。

\displaystyle H(X) = -\int_{-\infty}^{\infty}p(x)\ln{p(x)} dx
直感的には、次に得られる情報量がどれだけの価値がある可能性があるかを示している数値になります。
（情報量とは、確率的に低いものを得た時に情報量を多く得たと判断するものです。）

KLダイバージェンス

今、正しい確率分布 p(x) と、その確率分布を近似したモデルである q(x) があるとします。
この時に、 q(x) によって真の値を推測するために追加で必要な情報量の平均として定義されます。
具体的には、次のように表されます。「 q(x) のエントロピー- p(x) のエントロピー」と捉えるとわかりやすいかもしれません。
{\displaystyle KL(p||q) = -\int_{-\infty}^{\infty}p(x)\ln{\frac{q(x)}{p(x)}}dx }

描画してみる

対象とするモデル

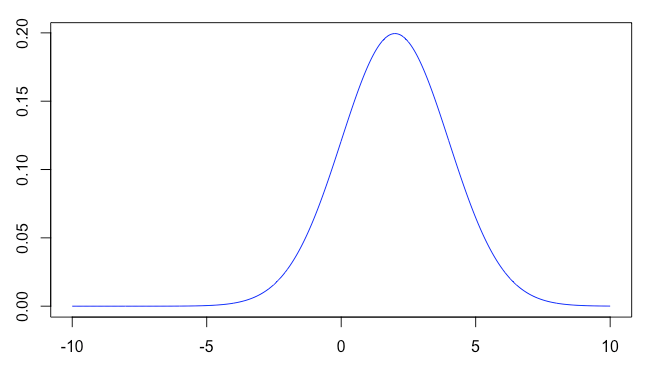
以下のように、平均mean2=2, 標準偏差sd2=2の正規分布を対象とします。

X = seq(-10, 10, length = n)
Y4 = dnorm(X, mean = mean2, sd = sd2)
plot(X,
Y4,
type = "l",
col = "blue")

f:id:thescript1210:20180501005147p:plain

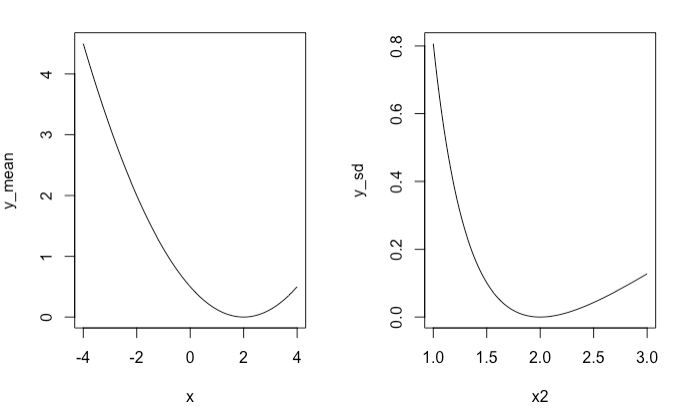
KLダイバージェンスの図示

左の図は平均値を変化させた時のKLダイバージェンスの値。平均値が対象モデルと同じ2の時にKLダイバージェンスは最小値を取ることがわかります。
右の図は標準偏差を変化させた時のKLダイバージェンスの値。標準偏差が対象モデルと同じ2の時にKLダイバージェンスは最小値を取ることがわかります。

これらのことから、KLダイバージェンスは、モデル間のパラメータを用いて、モデル間の距離を表していると捉えることができますね。

f_kl_divergence = function(m1, m2, sd1, sd2) {
  log(sd1 / sd2) + (sd2 ^ 2 + (m1 - m2) ^ 2) / (2 * sd1 ^ 2) - 1 / 2
}
y_mean = c()
x = seq(-4, 4, length = 100)
for (i in x) {
y_mean = append(y_mean, f_kl_divergence(i, mean2, sd2, sd2))
}

y_sd = c()
x2 = seq(1, 3, length = 100)
for (i in x2) {
   y_sd = append(y_sd, f_kl_divergence(mean2, mean2, i, sd2))
}

layout(matrix(1:2, ncol=2))
plot(x, y_mean, type="l")
plot(x2, y_sd, type="l")

f:id:thescript1210:20180501005336p:plain

（番外編）Rのライブラリを用いてみる

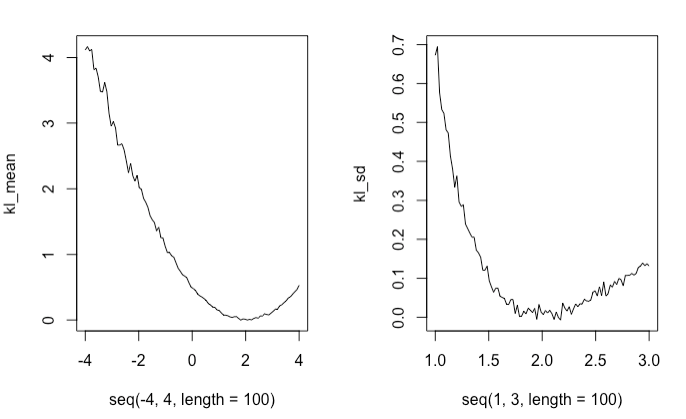
Rには、KLダイバージェンスにしたがって乱数を生成し、元モデルのパラメータを推定する関数があります。
その関数であるKL.divergence()を用いて乱数を発生させ、それをプロットしました。

するとその結果は先ほどplotした理論値に近いグラフを描画することができました。

library(FNN)
set.seed(100)

kl_mean = c()
Y1 =  rnorm(n * 10, mean = mean2, sd = sd2)
for (i in seq(-4, 4, length = 100)) {
  Y2 = rnorm(n * 10, mean = i, sd = sd2)
  divs = KL.divergence(Y1, Y2, k = 2)
  kl_mean = append(kl_mean, mean(divs))
}

kl_sd = c()
for (i in seq(1, 3, length = 100)) {
  Y3 = rnorm(n * 10, mean = mean2, sd = i)
  divs2 = KL.divergence(Y1, Y3, k = 2)
  kl_sd = append(kl_sd, mean(divs2))
}

layout(matrix(1:2, ncol=2))
plot(seq(-4, 4, length = 100), kl_mean, type="l")
plot(seq(1, 3, length = 100), kl_sd, type="l")

f:id:thescript1210:20180501005418p:plain